2  Understanding Data Structures

In this Lab 2, we’ll explore the fundamental data structures that are essential for data analysis in R: vectors, matrices, data frames, and lists. Mastering these structures will enable you to handle data efficiently and perform various operations crucial for statistical analysis and data science tasks.

By the end of this lab, you will be able to:

By completing Lab 2, you’ll build a solid foundation in handling data structures in R, which is crucial for more advanced data analysis and programming tasks.

2.1 Introduction

R offers several fundamental data structures to handle diverse data and analytical needs. These include vectors, matrices, factors, data frames, and lists.

An infographic showing the four core data structures in R: Vector, List, Matrix, and Data Frame. The R logo is positioned at the center, with arrows pointing toward each of the data structures, indicating their central role in data handling within R programming.
Figure 2.1: Data Structures in R Programming

2.2 Experiment 2.1: Vectors

A vector is a one-dimensional array that holds elements of the same data type. This is the most basic and frequently used data structure in R.

An infographic illustrating the different types of vectors in R programming. The diagram highlights five vector types: Logical (TRUE, FALSE), Numeric (5, 3.14), Integer (2L, 34L, 0L), Complex (3 + 2i), and Character ('a', 'Hello', 'True'). Each type is represented with examples, demonstrating how R categorizes different data elements in vectors.
Figure 2.2: Types of Vectors in R Programming

2.2.1 Creating a Vector

To create a vector, use the c() function:

gender <- c("Male", "Female", "Female", "Male", "Female", "Male")

Adding a space after every comma in c() makes your code more readable:

covid_confirmed <- c(31, 30, 37, 25, 33, 34, 26, 32, 23, 45)

covid_confirmed
#>  [1] 31 30 37 25 33 34 26 32 23 45

You can check the class of the vector using the class() function:

class(covid_confirmed)
#> [1] "numeric"

2.2.2 Factor vectors

A categorical variable where each level is a category will be of type factor. For example, gender is a categorical variable with two levels: “Male” or “Female”.

You can create a factor vector directly using the factor() function:

gender_factor <- factor(c("Male", "Female", "Female", "Male", "Female"))

gender_factor
#> [1] Male   Female Female Male   Female
#> Levels: Female Male

Check the class and levels:

class(gender_factor) # Returns "factor"
#> [1] "factor"
levels(gender_factor) # Returns "Female" "Male"
#> [1] "Female" "Male"

If you already have a character vector, convert it to a factor vector using as.factor():

gender <- c("Male", "Female", "Female", "Male", "Female")

gender_factor <- as.factor(gender)

gender_factor
#> [1] Male   Female Female Male   Female
#> Levels: Female Male
class(gender_factor)
#> [1] "factor"
levels(gender_factor)
#> [1] "Female" "Male"

2.2.3 Length of a vector

Find the length of a vector using the length() function:

covid_confirmed <- c(31, 30, 37, 25, 33, 34, 26, 32, 23, 45)

length(covid_confirmed)
#> [1] 10

2.2.4 Arithmetic Operations with Vectors

Operations with vector are performed element-wise.

egg_weight1 <- c(59, 56, 61, 68, 52, 53, 69, 54, 57, 51)

egg_weight2 <- c(56, 51, 69, 52, 57, 68, 61, 54, 59, 53)

total_weight <- egg_weight1 + egg_weight2

total_weight
#>  [1] 115 107 130 120 109 121 130 108 116 104

2.2.5 Vector selection

To select elements of a vector, use square brackets [ ] and indicate the index of elements to select. R indexing starts at 1.

For example:

Weekday Monday Tuesday Wednesday Thursday Friday Saturday Sunday
index 1 2 3 4 5 6 7 
weekday <- c("Monday", "Tuesday", "Wednessday", "Thursday", "Friday", "Saturday", "Sunday")

Access the first element:

weekday[1]
#> [1] "Monday"

Access the second element:

weekday[2]
#> [1] "Tuesday"

2.2.6 Exercise 2.1.1: Vector Selection

Given the quiz scores of 13 students:

10, 15, 10, 9, 18, 16, 14, 12, 16, 13, 15, 20, 17.

  • Create a vector named score containing the data.

  • Access individual scores of the 1st, 5th, and 10th students.

  • Access them all together.

2.3 Experiment 2.2: Matrices

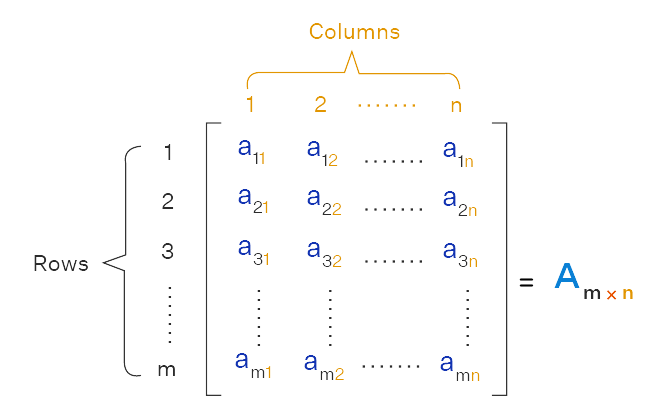
A matrix is a two-dimensional data structure consisting of a rectangular array of elements of the same data type, organized into rows and columns. Figure 2.3 illustrates how matrices are typically represented in mathematics.

A diagram illustrating the structure of a matrix with m rows and n columns. Each element is represented by (a_{ij}), where (i) indicates the row and (j) indicates the column. The matrix is denoted as (A_{m \times n}), showing its dimensions as m by n. The diagram breaks down the elements into rows and columns, explaining the arrangement of data within a matrix.
Figure 2.3: Matrix Representation in Linear Algebra

2.3.1 Creating Matrices

To create a matrix, use the matrix() function:

matrix(data, nrow, ncol, byrow = FALSE)

where:

  • data: Elements to arrange in the matrix.

  • nrow: Number of rows.

  • ncol: Number of columns.

  • byrow: Fill matrix by rows if TRUE.

Create the matrix A:

\[A = \begin{pmatrix} 1&-2& 5\\ -3&9&4\\ 5&0&6 \end{pmatrix}\]

A <- matrix(c(1, -2, 5, -3, 9, 4, 5, 0, 6), nrow = 3, ncol = 3, byrow = TRUE)

print(A)
#>      [,1] [,2] [,3]
#> [1,]    1   -2    5
#> [2,]   -3    9    4
#> [3,]    5    0    6

Create the matrix B:

\[B = \begin{pmatrix} 2&-8& 14\\ 4&10&16\\ 6&12&18 \end{pmatrix}\]

B <- matrix(c(2, 4, 6, -8, 10, 12, 14, 16, 18), nrow = 3, ncol = 3, byrow = FALSE)

print(B)
#>      [,1] [,2] [,3]
#> [1,]    2   -8   14
#> [2,]    4   10   16
#> [3,]    6   12   18

2.3.2 Matrices slicing

Accessing elements in a matrix is done by using [row, column], between the square brackets, you indicate the position of the row and column in which the elements to access are. For example, to access the element in the first row and second column of matrix A, you type A[1, 2]. To access the element in the third row and second column of matrix A, you type A[3, 2].

A[1, 2] # Element in first row, second column
#> [1] -2
A[3, 2] # Element in third row, second column
#> [1] 0

2.3.3 Arithmetic Operation in Matrices

You can perform arithmetic operations on matrices. Consider the following matrices

\[A = \begin{pmatrix} 1&-2& 5\\ -3&9&4\\ 5&0&6 \end{pmatrix}\]

\[B = \begin{pmatrix} 2&-8& 14\\ 4&10&16\\ 6&12&18 \end{pmatrix}\]

A <- matrix(c(1, -3, 5, -2, 9, 0, 5, 4, 6), nrow = 3, ncol = 3, byrow = FALSE)
B <- matrix(c(2, 4, 6, 8, 10, 12, 14, 16, 18), nrow = 3, ncol = 3, byrow = FALSE)

Addition

A + B
#>      [,1] [,2] [,3]
#> [1,]    3    6   19
#> [2,]    1   19   20
#> [3,]   11   12   24

Multiplication

Matrix multiplication is done using %*% operator:

A %*% B
#>      [,1] [,2] [,3]
#> [1,]   24   48   72
#> [2,]   54  114  174
#> [3,]   46  112  178

2.3.4 Exercise 2.2.1: Matrix Transpose

Consider the following matrix \(A\):

\[A = \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{pmatrix}\]

Your Task:

Find the transpose of matrix \(A\), denoted as \(A^{T}\).

Tip

Define matrix \(A\), then use t(A) to find its transpose.

Here’s a starting point for your code:

# Define matrix A

A <- matrix(c(...), nrow = ..., ncol = ..., byrow = TRUE)

A_transpose <- ...(A)

Replace the ... with the correct values and complete the exercise!

2.3.5 Exercise 2.2.2: Matrix Inverse Multiplication

Given the matrices \(A\) and \(B\) below:

\[A = \begin{pmatrix} 4 & 7 \\ 2 & 6 \end{pmatrix}\]

\[ B = \begin{pmatrix} 3 & 5 \\ 1 & 2 \end{pmatrix}\]

Your Task:

Calculate \(A^{-1} \times B\), where \(A^{-1}\) is the inverse of matrix \(A\).

Hint:

  • Use the solve() function in R to find the inverse of matrix \(A\).

  • Use the matrix multiplication operator %*% to multiply \(A^{-1}\) by \(B\).

Here’s a starting point for your code:

# Define matrices A and B
A <- matrix(c(...), nrow = ..., ncol = ..., byrow = TRUE)
B <- matrix(c(...), nrow = ..., ncol = ..., byrow = TRUE)

# Find the inverse of A
A_inverse <- solve(A)

# Multiply A_inverse by B
result <- A_inverse %*% B

Replace the ... with the correct values for your matrices and complete the exercise!

2.4 Experiment 2.3: Data frame

A data frame is a versatile table-like structure, allowing columns of different data types. It has variables as columns and observations as rows, similar to a spreadsheet or a SQL table.

2.4.1 Creating a Data Frame

To create a data frame, use the data.frame() function:

demographic_data <- data.frame(
  age = c(16, 18, 13, 17, 22),
  gender = c("Female", "Female", "Male", "Female", "Male"),
  bank_account = c(TRUE, FALSE, FALSE, TRUE, FALSE)
)

demographic_data

The number 1 2 3 4 5 at the left hand side on your console are row labels. Also, each column in a data frame is a vector.

Example: COVID 19 Data Frame

Create a data frame with columns states, confirmed cases, recovered cases and death cases.

states <- c("Lagos", "FCT", "Plateau", "Kaduna", "Rivers", "Oyo")

confirmed_cases <- c(58033, 19753, 9030, 8998, 7018, 6838)

recovered_cases <- c(56990, 19084, 8967, 8905, 6875, 6506)

death_cases <- c(439, 165, 57, 65, 101, 123)

covid_19 <- data.frame(states, confirmed_cases, recovered_cases, death_cases)

covid_19

2.4.2 Exploring Data Frames

When working with large datasets, it’s useful to show only part of the data.

1. head(): Shows the first observations.

2. tail(): Shows the last observations.

Both head() and tail() print a top line called header, which contains the names of the different variables in your data set.

Another method that is often used to get a rapid overview of your dataset is the function str().

3. str(): shows you the structure of your dataset. The structure of a data frame tells you:

  • The total number of observations
  • The total number of variables
  • A full list of the variables names
  • The first observations

Applying the str() function will often be the first thing that you do when receiving a new dataset. It is a great way to get more insight in your dataset before diving into the real analysis.

4. names(): Prints each column name.

5. nrow(): Returns the number of rows.

6. ncol(): Returns the number of columns.

7. dim(): Returns the number of rows and columns.

8. View(): Opens a spreadsheet-style data viewer (in RStudio).

9. summary(): Returns summary statistics of all columns.

Consider the following vectors:

set.seed(2021) # For reproducibility

gender <- sample(c("Male", "Female"), 120, replace = TRUE)

height <- floor(rnorm(n = 120, mean = 3, sd = 0.5))

weight <- ceiling(rnorm(n = 120, mean = 55, sd = 9))

bmi <- weight / height^2

Create a data frame:

medical_data <- data.frame(gender, height, weight, bmi)

2.4.3 Explore the data

First six observations:

head(medical_data)

Last six observations:

tail(medical_data) # To get the last 6 observation

Column names:

names(medical_data)
#> [1] "gender" "height" "weight" "bmi"

You can also use:

colnames(medical_data)
#> [1] "gender" "height" "weight" "bmi"

View the dataset (in RStudio):

View(medical_data)
A data frame preview in RStudio showing columns for gender, height, weight, and BMI (body mass index). The table includes both male and female entries, with height, weight, and calculated BMI values for each individual. The data illustrates how categorical and numerical values can be organized and analyzed in R.
Figure 2.4: Data Frame Preview in RStudio: Gender, Height, Weight, and BMI

Descriptive statistics:

summary(medical_data)
#>     gender              height          weight           bmi        
#>  Length:120         Min.   :1.000   Min.   :37.00   Min.   : 2.375  
#>  Class :character   1st Qu.:2.000   1st Qu.:50.00   1st Qu.: 6.333  
#>  Mode  :character   Median :2.000   Median :56.00   Median :11.000  
#>                     Mean   :2.433   Mean   :55.58   Mean   :12.384  
#>                     3rd Qu.:3.000   3rd Qu.:62.00   3rd Qu.:14.312  
#>                     Max.   :4.000   Max.   :78.00   Max.   :63.000

2.4.4 Built-in Datasets

There are several ways to find the included datasets in R. Using data() will give you a list of available dataset.

A terminal output listing various built-in datasets in the R 'datasets' package. Examples include 'AirPassengers' (monthly airline passenger numbers from 1949-1960), 'CO2' (carbon dioxide uptake in grass plants), 'Titanic' (survival of passengers on the Titanic), and many others covering topics such as biology, finance, and historical data. This list highlights the variety of real-world data readily available for analysis in R.
Figure 2.5: Sample Datasets Available in the R ‘datasets’ Package

For example, to load the built-in dataset iris, use:

data("iris")

head(iris)

and to load the built-in dataset airquality, use:

data("airquality")

head(airquality)

To get help on a built-in dataset, such as airquality, use:

?airquality
A screenshot of the R documentation for the 'airquality' dataset, which provides daily air quality measurements in New York from May to September 1973. The dataset contains 153 observations on six variables: Ozone (ppb), Solar.R (Solar Radiation in Lang), Wind (mph), Temp (degrees Fahrenheit), Month (1-12), and Day (1-31). The documentation includes details about the data collection, usage, format, and sources of the dataset.
Figure 2.6: Airquality Dataset Documentation in R

2.4.5 Subsetting Data Frames

Every column in a data frame has a name and if you can recall, we can print the names attribute of a data frame, iris, by using:

names(iris)
#> [1] "Sepal.Length" "Sepal.Width"  "Petal.Length" "Petal.Width" 
#> [5] "Species"

and to access a specific column in a data frame by name, you will use the $ operator in the form of df$colname, where df is the name of the data frame and colname is the name of the column you are interested in. This operation will then return the column you want as a vector.

Access specific columns using the $ operator

Use the $ operator to get a vector of Sepal.Length from the iris data frame:

iris$Sepal.Length
#>   [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9 5.4 4.8 4.8 4.3 5.8 5.7 5.4 5.1
#>  [19] 5.7 5.1 5.4 5.1 4.6 5.1 4.8 5.0 5.0 5.2 5.2 4.7 4.8 5.4 5.2 5.5 4.9 5.0
#>  [37] 5.5 4.9 4.4 5.1 5.0 4.5 4.4 5.0 5.1 4.8 5.1 4.6 5.3 5.0 7.0 6.4 6.9 5.5
#>  [55] 6.5 5.7 6.3 4.9 6.6 5.2 5.0 5.9 6.0 6.1 5.6 6.7 5.6 5.8 6.2 5.6 5.9 6.1
#>  [73] 6.3 6.1 6.4 6.6 6.8 6.7 6.0 5.7 5.5 5.5 5.8 6.0 5.4 6.0 6.7 6.3 5.6 5.5
#>  [91] 5.5 6.1 5.8 5.0 5.6 5.7 5.7 6.2 5.1 5.7 6.3 5.8 7.1 6.3 6.5 7.6 4.9 7.3
#> [109] 6.7 7.2 6.5 6.4 6.8 5.7 5.8 6.4 6.5 7.7 7.7 6.0 6.9 5.6 7.7 6.3 6.7 7.2
#> [127] 6.2 6.1 6.4 7.2 7.4 7.9 6.4 6.3 6.1 7.7 6.3 6.4 6.0 6.9 6.7 6.9 5.8 6.8
#> [145] 6.7 6.7 6.3 6.5 6.2 5.9

Use the $ operator to get a vector of Species from the iris data frame:

iris$Species
#>   [1] setosa     setosa     setosa     setosa     setosa     setosa    
#>   [7] setosa     setosa     setosa     setosa     setosa     setosa    
#>  [13] setosa     setosa     setosa     setosa     setosa     setosa    
#>  [19] setosa     setosa     setosa     setosa     setosa     setosa    
#>  [25] setosa     setosa     setosa     setosa     setosa     setosa    
#>  [31] setosa     setosa     setosa     setosa     setosa     setosa    
#>  [37] setosa     setosa     setosa     setosa     setosa     setosa    
#>  [43] setosa     setosa     setosa     setosa     setosa     setosa    
#>  [49] setosa     setosa     versicolor versicolor versicolor versicolor
#>  [55] versicolor versicolor versicolor versicolor versicolor versicolor
#>  [61] versicolor versicolor versicolor versicolor versicolor versicolor
#>  [67] versicolor versicolor versicolor versicolor versicolor versicolor
#>  [73] versicolor versicolor versicolor versicolor versicolor versicolor
#>  [79] versicolor versicolor versicolor versicolor versicolor versicolor
#>  [85] versicolor versicolor versicolor versicolor versicolor versicolor
#>  [91] versicolor versicolor versicolor versicolor versicolor versicolor
#>  [97] versicolor versicolor versicolor versicolor virginica  virginica 
#> [103] virginica  virginica  virginica  virginica  virginica  virginica 
#> [109] virginica  virginica  virginica  virginica  virginica  virginica 
#> [115] virginica  virginica  virginica  virginica  virginica  virginica 
#> [121] virginica  virginica  virginica  virginica  virginica  virginica 
#> [127] virginica  virginica  virginica  virginica  virginica  virginica 
#> [133] virginica  virginica  virginica  virginica  virginica  virginica 
#> [139] virginica  virginica  virginica  virginica  virginica  virginica 
#> [145] virginica  virginica  virginica  virginica  virginica  virginica 
#> Levels: setosa versicolor virginica

Because the $ operator returns a vector, you can easily calculate descriptive statistics on columns of a data frame by applying your favorite vector function (like mean(), sd(), or table()) to a column using $.

Let’s calculate the mean of Sepal.Length with themean() function and the frequency of each Species with the table()function in the iris data frame:

mean(iris$Sepal.Length)
#> [1] 5.843333
table(iris$Species)
#> 
#>     setosa versicolor  virginica 
#>         50         50         50

Access elements using [row, column]

Just like a matrix, you can access specific data in a data frame by using [row, column], where rows and columns are vectors of integers.

Data Frame Slicing Interpretation
data[1, ] First row and all columns
data[, 2] All rows and second column
data[c(1, 3, 5), 2] Rows 1, 3, 5 and column 2 only
data[1:3, c(1, 3)] First three rows and columns 1 and 3 only
data or data[, ] All rows and all columns
Data Frame Slicing in R
Examples and Interpretations
Data Frame Slicing Interpretation
data[1, ] First row and all columns
data[, 2] All rows and second column
data[c(1, 3, 5), 2] Rows 1, 3, 5 and column 2 only
data[1:3, c(1, 3)] First three rows and columns 1 and 3 only
data or data[, ] All rows and all columns

2.4.6 Exercise 2.3.1: Subsetting a Dataframe

Using the airquality dataset:

  • Examine the airquality dataset.

  • Select the first three columns.

  • Select rows 1-3 and columns 1 and 3.

  • Select rows 1-5 and column 1.

  • Select the first row.

  • Select the first 6 rows .

2.5 Experiment 2.4: Lists

A list in R is like a container that can hold various elements, such as vectors, matrices, data frames, and even other lists.

2.5.1 Creating a List

Use the list() function to create a list:

my_list <- list(
  age = 19,
  gender = "Male",
  pass = TRUE
)

Here, my_list consists of three components:

  • age: Numeric value.

  • gender: Character string.

  • pass: Logical value.

2.5.2 Accessing List Elements

To show the contents of a list you can simply type its name as any other object in R:

my_list
#> $age
#> [1] 19
#> 
#> $gender
#> [1] "Male"
#> 
#> $pass
#> [1] TRUE

You can extract individual element in a list by using double square brackets [[ ]]. For example,

my_list[[1]] # Returns 19
#> [1] 19
my_list[["age"]] # Returns 19
#> [1] 19

Using single square brackets [ ] returns a list containing the element.

my_list[1]
#> $age
#> [1] 19

2.6 Summary

In this lab 2, you have acquired foundational skills in R’s basic data structures:

  • Understanding the characteristics and differences between vectors, matrices, data frames, and lists.

  • Creating and manipulating these data structures effectively.

  • Accessing and modifying data elements within each structure using appropriate indexing and functions.

These skills are essential for any data analysis or data science task in R, and they form the basis for more advanced topics that you will encounter as you continue learning. Congratulations on building this crucial foundation!

In the next lab, you’ll explore how to write your own functions in R. Functions are a powerful tool that will help you streamline your code, automate tasks, and make your programs more efficient. Get ready to enhance your programming skills by learning how to create custom functions!