2  Understanding Data Structures

2.1 Introduction

Welcome to Lab 2! In this lab, we’ll delve into the fundamental data structures in R that are essential for data analysis and manipulation. Understanding these data structures will empower you to handle data efficiently and perform various operations crucial for statistical analysis and data science tasks.

2.2 Learning Objectives

By completing this lab, you will be able to:

  • Identify Fundamental Data Structures
    Recognize and describe the key characteristics of vectors, matrices, data frames, and lists in R.

  • Create Data Structures
    Construct vectors, matrices, data frames, and lists using appropriate functions and syntax in R.

  • Manipulate Data Structures
    Perform operations such as indexing, slicing, and modifying elements within vectors, matrices, data frames, and lists.

  • Apply Appropriate Operations and Functions
    Utilize relevant R functions and operators to perform calculations and transformations specific to each data type.

  • Demonstrate Understanding Through Application
    Solve problems and complete exercises that require the correct application of operations and functions to manipulate and analyze data within these structures.

By completing this lab, you’ll have a solid foundation in working with vectors, matrices, data frames, and lists, setting you up for success in more advanced topics.

2.3 Prerequisites

Before starting this lab, you should have:

  • Completed Lab 1 or have basic knowledge of R programming fundamentals.

  • Familiarity with basic arithmetic operations and variable assignment in R.

  • An interest in learning how to manage and manipulate data effectively.

2.4 Exploring Data Structures in R

R offers several fundamental data structures to handle diverse data and analytical needs. These include vectors, matrices, data frames, and lists.

An infographic showing the four core data structures in R: Vector, List, Matrix, and Data Frame.
Figure 2.1: Data Structures in R Programming

2.5 Experiment 2.1: Vector

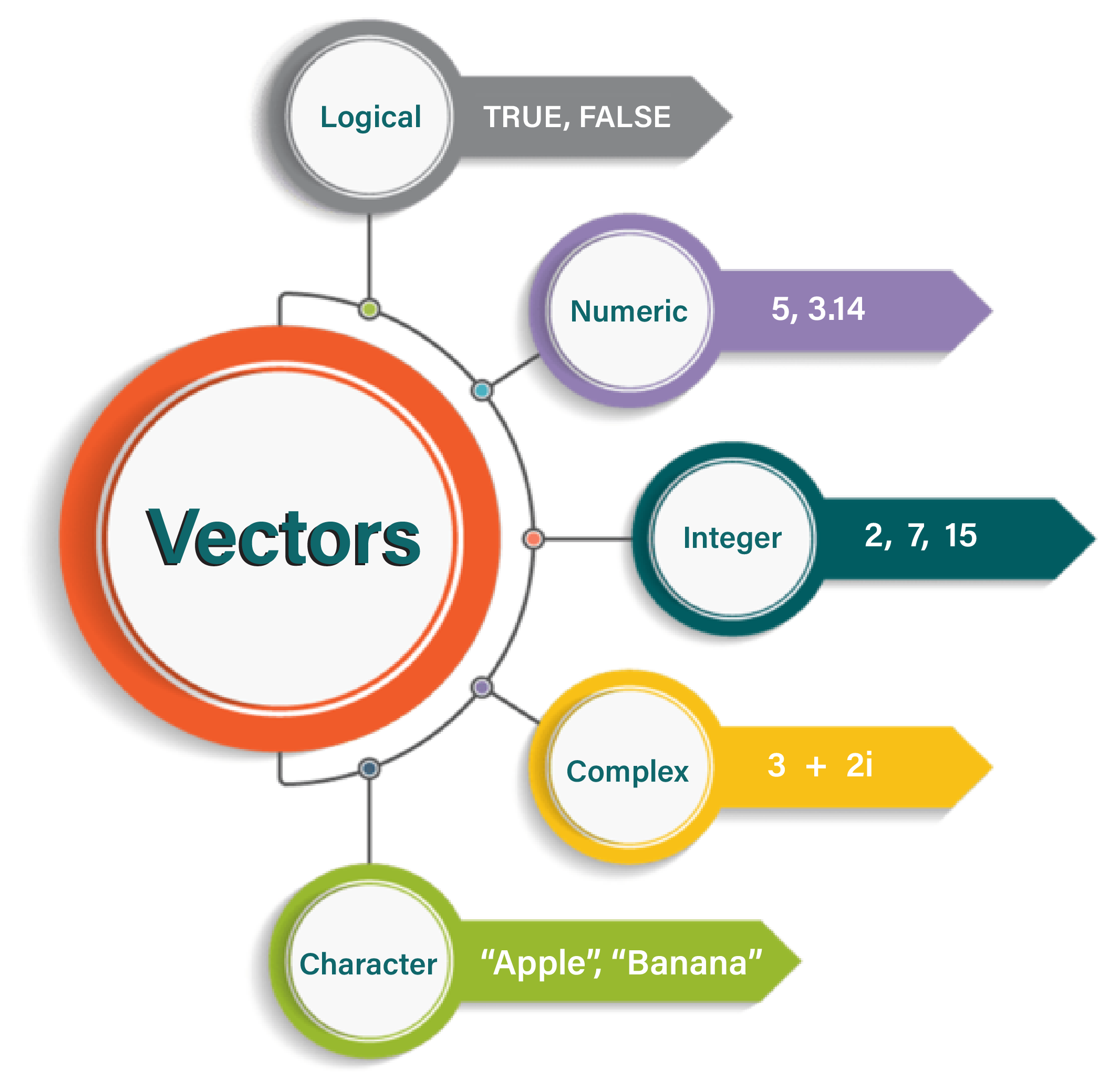
A vector is a one-dimensional array in R that stores elements of the same data type. Vectors are the most basic and frequently used data structures in R and are essential for data manipulation and analysis.

An infographic illustrating the different types of vectors in R programming. The diagram highlights five vector types: Logical (TRUE, FALSE), Numeric (5, 3.14), Integer (2L, 34L, 0L), Complex (3 + 2i), and Character ('a', 'Hello', 'True'). Each type is represented with examples, demonstrating how R categorizes different data elements in vectors.
Figure 2.2: Types of Vectors in R Programming

2.5.1 Creating a Vector

You can create a vector in R using the c() function1, which stands for “combine” or “concatenate.”

Example 1: Eye Colour

eye_colour <- c("Green", "Blue", "Brown", "Green", "Green", "Brown", "Blue")

eye_colour
#> [1] "Green" "Blue"  "Brown" "Green" "Green" "Brown" "Blue"

Here, eye_colour is a character vector, as it contains text values and the c() function makes it easy to combine individual elements into a single vector.

Best Practice:

When using the c() function, it’s a good practice to add a space after each comma. This makes your code cleaner and easier to read.

Example 2: Product Prices

# Vector of product prices in USD

product_prices <- c(19.99, 5.49, 12.89, 99.99, 49.95)

product_prices
#> [1] 19.99  5.49 12.89 99.99 49.95

2.5.2 Checking the Type of a Vector

To determine the data type of a vector, use the class() function:

class(product_prices)
#> [1] "numeric"

2.5.3 Length of a Vector

The length of a vector refers to the total number of elements it contains. You can determine this using the length() function, which returns an integer representing the total count of elements in the vector.

covid_confirmed <- c(31, 30, 37, 25, 33, 34, 26, 32, 23, 45)

length(covid_confirmed)
#> [1] 10

2.5.4 Advanced Vector Creation

While the simplest way to create a vector is by directly assigning values, R provides powerful tools for generating and manipulating vectors tailored to specific needs. This section explores advanced methods like :, c(), seq(), rep(), and sample() to create flexible, efficient, and custom vectors.

2.5.4.1 : Operator - Quick Sequence Generation

The : operator generates a sequence of integers between a starting and an ending value.

Syntax:

start:end

Where:

  • start: The starting value of the sequence.

  • end: The ending value of the sequence.

Examples:

  • Create a sequence from 1 to 10:

    sequence <- 1:10
sequence
    #>  [1]  1  2  3  4  5  6  7  8  9 10

  • Create a descending sequence:

    reverse_sequence <- 10:1
reverse_sequence
    #>  [1] 10  9  8  7  6  5  4  3  2  1
Use Case

The : operator is ideal for quickly generating ranges for indexing, loops, or other operations requiring consecutive integers.

2.5.4.2 c() Function - Vector Concatenation

The c() function combines individual elements or existing vectors into a single vector.

Syntax:

c(element1, element2, ..., elementN)

Where:

  • element1, element2, …, elementN: The individual values or vectors to be combined into a single vector.

Examples:

  • Combine numeric elements:

    numbers <- c(2, 4, 6, 8)
numbers
    #> [1] 2 4 6 8

  • Concatenate multiple vectors:

    vector1 <- c(1, 2, 3)
vector2 <- c(4, 5, 6)

combined <- c(vector1, vector2)
combined
    #> [1] 1 2 3 4 5 6

  • Combine mixed data types:

    mixed <- c(10, "Apple", TRUE)
mixed
    #> [1] "10"    "Apple" "TRUE"
Use Case

All elements are coerced to the same data type (character in this case). Use c() to append data, merge multiple vectors, or build vectors from scratch.

2.5.4.3 seq() Function - Custom Sequence Generation

The seq() function allows for more flexible sequence generation compared to the : operator. You can specify the step size or desired length of the sequence.

Syntax:

seq(from, to, by, length)

Where:

  • from: The starting value of the sequence.

  • to: The ending value of the sequence.

  • by: The increment (step size) between values. Defaults to 1 if not specified.

  • length: The desired number of elements in the sequence. Overrides by if specified.

Examples:

  • Generate a sequence with a positive step size:

    custom_step <- seq(1, 10, by = 2)
custom_step
    #> [1] 1 3 5 7 9

  • Generate a sequence with a negative non-integer step size:

    descending <- seq(5, 1, by = -0.5)
descending
    #> [1] 5.0 4.5 4.0 3.5 3.0 2.5 2.0 1.5 1.0

  • Generate a sequence of a specific length:

    custom_length <- seq(1, 10, length = 5)
custom_length
    #> [1]  1.00  3.25  5.50  7.75 10.00
Use Case

The seq() function is perfect for creating sequences with integer (non-integer) steps or evenly spaced data points.

2.5.4.4 rep() Function - Value Replication

The rep() function replicates values multiple times, creating patterns or duplications as needed.

Syntax:

rep(x, times, each)

Where:

  • x: The vector or value to be replicated.

  • times: The number of times to repeat the entire vector.

  • each: The number of times to repeat each element of the vector.

Examples:

  • Repeat a value multiple times:

    rep("God is good!", 5)
    #> [1] "God is good!" "God is good!" "God is good!" "God is good!"
#> [5] "God is good!"

  • Repeat a vector multiple times:

    rep(1:3, times = 2)
    #> [1] 1 2 3 1 2 3

  • Repeat each element of a vector:

    rep(c("Female", "Male"), each = 2)
    #> [1] "Female" "Female" "Male"   "Male"
Use Case

Use rep() to generate repetitive patterns for simulation, modeling, or experimental data.

2.5.4.5 sample() Function - Random Sampling

The sample() function generates random samples from a vector, with or without replacement.

Syntax:

sample(x, size, replace = FALSE, prob = NULL)

Where:

  • x: The vector to sample from.

  • size: The number of samples to draw.

  • replace: Logical; whether sampling is with replacement (TRUE) or without replacement (FALSE).

  • prob: A vector of probabilities for each element in x.

Examples:

  • Random sample without replacement:

    fruit <- c("Apple", "Banana", "Cherry", "Orange", "Pineapples", "Grape", "Pawpaw")

sample(x = fruit, size = 4)
    #> [1] "Pawpaw"     "Grape"      "Apple"      "Pineapples"

    Example output; results vary due to randomness

  • Random sample with replacement:

    sample(1:10, 5, replace = TRUE)
    #> [1] 9 1 6 7 1

    Example output; results vary due to randomness

Set a Seed for Reproducibility

When you perform random sampling in R, the results may vary each time you run the code. By using set.seed(), you ensure that the random number generator starts from the same point, producing consistent results every time the code is executed.

Examples

# Set a seed for consistent results
set.seed(123)

# Generate a random sample of 5 numbers
sample(1:10, 5)
#> [1]  3 10  2  8  6

This output will always be the same with set.seed(123)

  • Weighted Sampling:

    Weighted sampling is a method of random sampling where each element in the population is assigned a probability of being selected. These probabilities, or weights, determine the likelihood of an element being chosen, allowing certain elements to have a higher or lower chance of selection compared to others.

    Example:

    Let’s simulate 10 flips of a biased coin, where the probability of getting a Head (H) is \(0.7\) and the probability of a Tail(T) is \(0.3\).

    # Sample with probabilities

set.seed(1923)

coin_face <- c("H", "T") # Possible outcomes

prob <- c(0.7, 0.3) # Higher probability for "Head"

# Perform weighted sampling

sampled_prob <- sample(coin_face, prob = prob, size = 10, replace = TRUE)

sampled_prob
    #>  [1] "H" "H" "H" "H" "T" "T" "T" "T" "T" "H"
Use Case

Use sample() for bootstrapping, simulations, or creating random subsets from data.

2.5.5 Vector Operations

When working with vectors, most basic operations are applied element-by-element, making it both intuitive and efficient to transform and analyse collections of data.

2.5.5.1 Arithmetic Operations

Arithmetic operations on vectors are performed element-wise. For example, consider a vector of product prices:

# Vector of product prices in USD

product_prices <- c(19.99, 5.49, 12.89, 99.99, 49.95)

If we want to apply a \(10\%\) discount to all prices, we can multiply the entire vector by 0.9:

# Apply a discount of 10% to all product prices

discounted_prices <- product_prices * 0.9

discounted_prices
#> [1] 17.991  4.941 11.601 89.991 44.955

In this example, each element in product_prices is multiplied by \(0.9\), producing the discounted_prices vector.

Common Pitfall

  • Data Type Coercion: Mixing data types in a vector can lead to unexpected results.

  • Tip: Ensure all elements are of the same data type to avoid automatic coercion.

2.5.5.2 Mathematical and Statistical Functions

R provides many built-in functions that operate on vectors and return summary values or transformed vectors. These functions are vectorised, meaning they automatically apply to every element where relevant. Examples include:

  • sum(product_prices) – returns the sum of all prices.

  • mean(product_prices) – returns the average price.

  • max(product_prices) / min(product_prices) – returns the maximum or minimum value.

  • sd(product_prices) / var(product_prices) – returns the standard deviation or variance of the product prices.

  • round(product_prices, digits = 1) – rounds all prices to one decimal place.

2.5.5.3 Element-wise Functions

Functions like sqrt(), log(), exp(), and abs() apply mathematically to each element:

sqrt_prices <- sqrt(product_prices)
sqrt_prices
#> [1] 4.471018 2.343075 3.590265 9.999500 7.067531
log_prices <- log(product_prices)
log_prices
#> [1] 2.995232 1.702928 2.556452 4.605070 3.911023

2.5.5.4 Sorting and Ordering

You can also sort vectors or determine the order of elements:

product_prices <- c(19.99, 5.49, 12.89, 99.99, 49.95)

sorted_prices <- sort(product_prices)
sorted_prices
#> [1]  5.49 12.89 19.99 49.95 99.99

2.5.5.5 Vectorised Conditional Operations with ifelse()

The ifelse() statement is a vectorised conditional function in R. It evaluates a condition for each element of a vector, returning one value if the condition is TRUE and another value if it is FALSE. This makes it an essential function for data transformation and analysis.

Example 1: Categorise Product Prices

Suppose we have a vector of product prices in USD, and we want to categorise them as “Affordable” or “Expensive” based on whether they are below or above $50.

# Vector of product prices in USD
product_prices <- c(30, 75, 50, 20, 100)

# Categorise prices as "Affordable" or "Expensive"
price_category <- ifelse(product_prices < 50, "Affordable", "Expensive")

# Print the result
price_category
#> [1] "Affordable" "Expensive"  "Expensive"  "Affordable" "Expensive"

Example 2: Apply a Discount for Expensive Products

If a product price is above $50, apply a 10% discount. Otherwise, keep the price unchanged.

# Apply discount for products above $50
discounted_prices <- ifelse(product_prices > 50, product_prices * 0.9, product_prices)

# Print the result
discounted_prices
#> [1] 30.0 67.5 50.0 20.0 90.0

2.5.6 Vector selection

To select elements of a vector, use square brackets [] with the index of the element(s). R indexing starts at 1 (i.e. R uses 1-based indexing).

For example:

Weekday Monday Tuesday Wednesday Thursday Friday Saturday Sunday
index 1 2 3 4 5 6 7

Example 1

weekday <- c(
  "Monday", "Tuesday", "Wednessday", "Thursday", "Friday", "Saturday", "Sunday"
)

Access the first weekday:

weekday[1]
#> [1] "Monday"

Access the second weekday:

weekday[2]
#> [1] "Tuesday"

Access multiple elements

weekday[c(2, 4)]
#> [1] "Tuesday"  "Thursday"

2.5.7 Reflection Question 2.1.1

Why is it important to know that R uses 1-based indexing?

See the Solution to Reflection Question 2.1.1

In addition to selecting elements by their positions, you can select elements of a vector based on conditions using comparison operators. This method involves creating a logical vector of TRUE and FALSE values by applying a condition to the vector, and then using this logical vector to index the original vector.

Example 2

Let’s start with a numeric vector representing daily temperatures:

# Create a numeric vector of temperatures
temperatures <- c(72, 65, 70, 68, 75, 80, 78)

Select temperatures greater than 70 degrees:

# Apply the condition and select elements
temperatures[temperatures > 70]
#> [1] 72 75 80 78
Explanation

  • temperatures > 70 creates a logical vector: [TRUE, FALSE, FALSE, FALSE, TRUE, TRUE, TRUE].

  • temperatures[temperatures > 70] selects elements where the condition is TRUE.

Select temperature that are even.

temperatures[temperatures %% 2 == 0]
#> [1] 72 70 68 80 78
Explanation

  • temperatures %% 2 computes the remainder when each temperature is divided by 2.

  • temperatures %% 2 == 0 returns TRUE for even temperature.

Example 3

Using our weekday vector:

weekday <- c(
  "Monday", "Tuesday", "Wednesday", "Thursday", "Friday",
  "Saturday", "Sunday"
)

Select weekdays that are “Saturday” or “Sunday”:

# Create a logical vector for the condition
is_weekend <- weekday == "Saturday" | weekday == "Sunday"

# Select elements based on the condition
weekend_days <- weekday[is_weekend]

# Display the result
weekend_days
#> [1] "Saturday" "Sunday"
Explanation

  • weekday == "Sunday" returns [FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, TRUE].

  • Using | (logical OR) combines the two conditions.

  • The final logical vector is [FALSE, FALSE, FALSE, FALSE, FALSE, TRUE, TRUE].

Selecting Weekdays (Excluding Weekends)

# Create a logical vector for weekdays
is_weekday <- !(weekday %in% c("Saturday", "Sunday"))

# Select elements based on the condition
weekday_days <- weekday[is_weekday]

# Display the result
weekday_days
#> [1] "Monday"    "Tuesday"   "Wednesday" "Thursday"  "Friday"
Explanation

  • weekday %in% c("Saturday", "Sunday") checks if each element is in the vector c("Saturday", "Sunday").

  • The %in% operator returns [FALSE, FALSE, FALSE, FALSE, FALSE, TRUE, TRUE].

  • Using ! negates the logical vector to [TRUE, TRUE, TRUE, TRUE, TRUE, FALSE, FALSE].

Code Style Guidelines

  • Naming Conventions: Use descriptive variable names in snake_case.

  • Indentation: Use consistent indentation for readability.

  • Comments: Explain complex code with comments.

2.5.8 Exercise 2.1.1: Vector Selection

Given the monthly sales figures (in units) for a product over a year:

120, 135, 150, 160, 155, 145, 170, 180, 165, 175, 190, 200

Your Tasks:

  1. Create a vector named monthly_sales containing the data.

  2. Access the sales figures for March, June, and December.

  3. Find the sales figures that are less than 60

  4. Calculate the average sales for the first quarter (January to March).

  5. Extract the sales figures for the last month of each quarter of the year

See the Solution to Exercise 2.1.1

2.5.9 Factor Vectors

Factors are a fundamental data structure in R used to represent categorical variables, where each value belongs to a specific category or “level.” Unlike character vectors, factors store categorical data more efficiently and are essential in statistical modeling, especially when using functions like summary() or performing analyses that require categorical distinctions.

2.5.9.1 Why Use Factors?

  • Statistical Modeling: Factors are crucial in statistical modeling as they explicitly designate categorical variables, allowing R’s modeling functions to handle them appropriately.

  • Efficient Storage: Factors store categorical data more efficiently than character vectors by using integer codes under the hood.

  • Data Integrity: By restricting data to predefined categories (levels), factors help maintain data integrity and reduce errors due to invalid entries.

  • Using Factors in Plots: Factors are particularly useful when creating plots, as they allow for meaningful ordering of categories.

2.5.9.2 Creating a Factor Vector

You can create a factor vector using the factor() function, converting a character or numeric vector into a factor.

Example 1: Product Categories

Suppose we have a vector of product categories:

# Vector of product categories
product_categories <- c(
  "Electronics", "Clothing", "Electronics",
  "Furniture", "Clothing", "Electronics"
)

product_categories
#> [1] "Electronics" "Clothing"    "Electronics" "Furniture"   "Clothing"   
#> [6] "Electronics"

Converting to a factor:

# Convert to factor
product_categories_factor <- factor(product_categories)

# Display the factor vector
product_categories_factor
#> [1] Electronics Clothing    Electronics Furniture   Clothing    Electronics
#> Levels: Clothing Electronics Furniture

Inspecting the Factor Levels:

levels(product_categories_factor)
#> [1] "Clothing"    "Electronics" "Furniture"

Checking the Data Type:

class(product_categories_factor)
#> [1] "factor"

If you already have a character vector, you can convert it to a factor vector using the as.factor() function.

Example 2: Ethnicity Categories

ethnicity <- c(
  "African", "Asian", "Latin American", "African", "Latin American",
  "Asian", "African", "European"
)

ethnicity_factor <- as.factor(ethnicity)

ethnicity_factor
#> [1] African        Asian          Latin American African       
#> [5] Latin American Asian          African        European      
#> Levels: African Asian European Latin American
Note

The levels are automatically determined and sorted alphabetically unless specified otherwise.

2.5.9.3 Ordered Factors

Sometimes, categorical variables have a natural ordering (e.g., “Low” < “Medium” < “High”). In such cases, you can create an ordered factor by specifying the levels in the desired order and setting ordered = TRUE.

Example 3: Satisfaction Ratings

# Vector of satisfaction ratings

satisfaction_ratings <- c(
  "High", "Medium", "Low", "High",
  "Medium", "Low", "High"
)

# Create an ordered factor
satisfaction_factors <- factor(satisfaction_ratings,
  levels = c("Low", "Medium", "High"),
  ordered = TRUE
)

# Display the ordered factor
satisfaction_factors
#> [1] High   Medium Low    High   Medium Low    High  
#> Levels: Low < Medium < High

Checking the data type:

class(satisfaction_factors)
#> [1] "ordered" "factor"

2.5.9.4 Using summary() with Factors:

The summary() function provides a count of each category in a factor vector:

# Summarise the satisfaction factors

summary(satisfaction_factors)
#>    Low Medium   High 
#>      2      2      3

2.5.9.5 Converting Factors to Numeric Values

Be cautious when converting factors to numeric values. Direct conversion using as.numeric() will return the internal integer codes representing the factor levels, which may not correspond to the actual values you expect.

Incorrect Way:

# Incorrect conversion
as.numeric(product_categories_factor)
#> [1] 2 1 2 3 1 2
Tip

The numbers represent the position of each level in the levels attribute, not the original data.

Correct Way:

First, convert the factor to a character vector, then to numeric (if applicable):

# Correct conversion (if levels are numeric strings)
as.numeric(as.character(product_categories_factor))
#> Warning: NAs introduced by coercion
#> [1] NA NA NA NA NA NA
Warning

This will produce NAs because the levels are not numeric strings. For factors with numeric levels, this method works correctly.

Example with Numeric Levels:

# Numeric factor example
numeric_factor <- factor(c("1", "3", "5", "2"))

# Correct conversion
numeric_values <- as.numeric(as.character(numeric_factor))

numeric_values
#> [1] 1 3 5 2
Common Pitfalls

  • Unintended Ordering: By default, factors are unordered. If your categorical variable has a natural order, specify it using the levels argument and set ordered = TRUE.

    # Ordered factor example
factor_variable <- factor(c("Low", "Medium", "High"),
  levels = c("Low", "Medium", "High"),
  ordered = TRUE
)

  • Converting Factors: Always be cautious when converting factors to numeric types to avoid unexpected results. Use as.character() before as.numeric() if necessary.

  • Missing Levels: If you specify levels that are not present in your data, R will include them with a count of zero.

    feedback_ratings <- c(
  "Good", "Excellent", "Poor", "Fair",
  "Good", "Excellent", "Fair"
)

# Specifying extra levels
feedback_factors <- factor(feedback_ratings,
  levels = c("Poor", "Fair", "Good", "Very Good", "Excellent"),
  ordered = TRUE
)

# Summarise
summary(feedback_factors)
    #>      Poor      Fair      Good Very Good Excellent 
#>         1         2         2         0         2

Ensure that the levels you specify match the data or be aware that additional levels will appear with zero counts.

2.5.9.6 Removing Unused Factor Levels

When working with factors in R, you might encounter situations where, after subsetting your data, the factor levels still include categories that no longer exist in your dataset. These unused levels can lead to misleading analyses and cluttered visualizations. To ensure that your factor variables accurately reflect the data, it’s important to remove these unused levels. This can be easily achieved using the droplevels() function.

Why Remove Unused Levels?

  • Accurate Analysis: Statistical functions and models may misinterpret unused levels, affecting results.

  • Clean Visualizations: Plots and charts can display empty categories, making them confusing.

  • Data Integrity: Keeping only relevant levels ensures your data accurately represents the current state.

Example 1: Removing Unused Levels from a Factor

Suppose you have a factor vector representing customer feedback ratings:

# Original factor with all levels
feedback_ratings <- c(
  "Good", "Excellent", "Poor",
  "Fair", "Good", "Excellent", "Fair"
)

feedback_factors <- factor(feedback_ratings,
  levels = c("Poor", "Fair", "Good", "Excellent"),
  ordered = TRUE
)

# Display the original factor
feedback_factors
#> [1] Good      Excellent Poor      Fair      Good      Excellent Fair     
#> Levels: Poor < Fair < Good < Excellent

Now, you decide to exclude the “Poor” ratings from your analysis:

# Subset the data to exclude "Poor" ratings
subset_feedback <- feedback_factors[feedback_factors != "Poor"]

# Display the subsetted factor
subset_feedback
#> [1] Good      Excellent Fair      Good      Excellent Fair     
#> Levels: Poor < Fair < Good < Excellent
Observation

Even after subsetting, the level “Poor” remains in the levels attribute, despite not being present in the data.

Using droplevels() to Remove Unused Levels

To clean up the factor and remove any levels that are no longer used, apply the droplevels() function:

# Remove unused levels
subset_feedback <- droplevels(subset_feedback)

# Display the cleaned factor
subset_feedback
#> [1] Good      Excellent Fair      Good      Excellent Fair     
#> Levels: Fair < Good < Excellent

Now, the factor levels accurately reflect only the categories present in the data.

# Check the levels of the cleaned factor
levels(subset_feedback)
#> [1] "Fair"      "Good"      "Excellent"
Note

Always Check Levels After Subsetting: It’s good practice to check the levels of your factor variables after any subsetting operation.

# Check levels before and after dropping unused levels
levels(feedback_factors)
#> [1] "Poor"      "Fair"      "Good"      "Excellent"
levels(subset_feedback)
#> [1] "Fair"      "Good"      "Excellent"

Apply droplevels() to Data Frames: If your data frame contains factor columns and you’ve performed row-wise subsetting, you can apply droplevels() to the entire data frame to clean all factor columns at once.

# Assuming 'df' is your data frame
df_clean <- droplevels(df)

Use in Modeling and Visualization: Clean factor levels ensure that statistical models and plots accurately represent your data without misleading categories.

2.5.10 Reflection Question 2.1.2

  • How does converting character vectors to factors benefit data analysis in R?

  • When would you use a factor instead of a character vector in R?

See the Solution to Reflection Question 2.1.2

2.5.11 Practice Quiz 2.1

Question 1:

Which function is used to create a vector in R?

  1. vector()
  2. c()
  3. list()
  4. data.frame()

Question 2:

Given the vector:

v <- c(2, 4, 6, 8, 10)

What is the result of v * 3?

  1. c(6, 12, 18, 24, 30)
  2. c(2, 4, 6, 8, 10, 3)
  3. c(6, 12, 18, 24)
  4. An error occurs

Question 3:

In R, is the vector c(TRUE, FALSE, TRUE) considered a numeric vector?

  1. True
  2. False

Question 4:

What will be the output of the following code?

numbers <- c(1, 3, 5, 7, 9)
numbers[2:4]
  1. 1, 3, 5
  2. 3, 5, 7
  3. 5, 7, 9
  4. 2, 4, 6

Question 5:

Which of the following best describes a factor in R?

  1. A numerical vector
  2. A categorical variable with predefined levels
  3. A two-dimensional data structure
  4. A list of vectors

Question 6:

Which function is used to create sequences including those with either integer or non-integer steps?

  1. :
  2. seq()
  3. rep()
  4. sample()

Question 7:
What does the following code output?

seq(10, 1, by = -3)
  1. 10, 7, 4, 1
  2. 10, 7, 4
  3. 1, 4, 7, 10
  4. An error occurs

Question 8:

Suppose you want to create a vector that repeats the sequence 1, 2, 3 five times. Which code will achieve this?

  1. rep(c(1, 2, 3), each = 5)
  2. rep(c(1, 2, 3), times = 5)
  3. rep(1:3, times = 5)
  4. rep(1:3, each = 5)

Question 9:

Suppose you are drawing coins from a treasure chest. There are 100 coins in this chest: 20 gold, 30 silver, and 50 bronze. Use R to draw 5 random coins from the chest. Use set.seed(50) to ensure reproducibility.

What will be the output of the random draw?

  1. Silver, Bronze, Bronze, Bronze, Silver
  2. Gold, Gold, Silver, Bronze, Bronze
  3. Gold, Bronze, Bronze, Bronze, Silver
  4. Silver, Bronze, Gold, Bronze, Bronze

Question 10:

What will the following code produce?

c(1, 2, 3) + c(4, 5)
  1. 5, 7, 8
  2. 5, 7, 7
  3. An error due to unequal vector lengths
  4. 5, 7, 9

See the Solution to Quiz 2.1

2.5.12 Exercise 2.1.2: Vector and Factor Manipulation

Given a vector of customer feedback ratings: c("Good", "Excellent", "Poor", "Fair", "Good", "Excellent", "Fair")

Your Tasks:

  1. Create a vector named feedback_ratings containing the data.

  2. Convert feedback_ratings into an ordered factor with levels: “Poor” < “Fair” < “Good” < “Excellent”.

  3. Summarize the feedback ratings.

  4. Identify how many customers rated “Excellent”.

See the Solution to Exercise 2.1.2

2.6 Experiment 2.2: Matrices

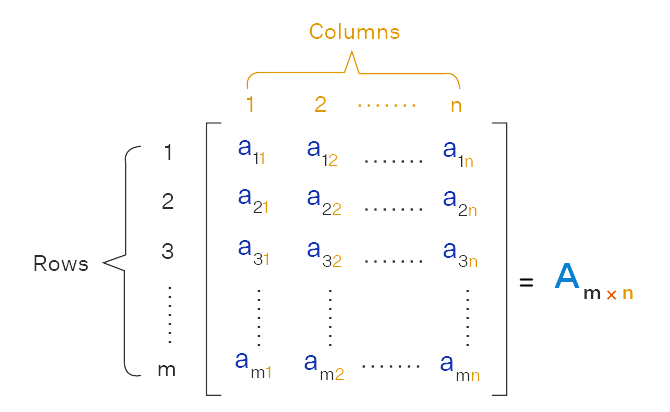
A matrix is a two-dimensional data structure consisting of a rectangular array of elements of the same data type, organized into rows and columns. Matrices are used extensively in linear algebra and statistical computations. Figure 2.3 illustrates a typical representation of a matrix.

A diagram illustrating the structure of a matrix with m rows and n columns. Each element is represented by $a_{ij}$, where (i) indicates the row and (j) indicates the column. The matrix is denoted as $A_{m \times n}$, showing its dimensions as m by n. The diagram breaks down the elements into rows and columns, explaining the arrangement of data within a matrix.
Figure 2.3: Matrix Representation in Linear Algebra

2.6.1 Creating Matrices

To create a matrix, use the matrix() function:

#|
matrix(data, nrow, ncol, byrow = FALSE)

where:

  • data: The elements to be arranged in the matrix.

  • nrow: The number of rows.

  • ncol: The number of columns.

  • byrow: If set to FALSE (the default), fills the matrix by columns; if set to TRUE, fills the matrix by rows.

Create the matrix A:

\[A = \begin{pmatrix} 1&-2& 5\\ -3&9&4\\ 5&0&6 \end{pmatrix}\]

A <- matrix(c(1, -2, 5, -3, 9, 4, 5, 0, 6), nrow = 3, ncol = 3, byrow = TRUE)

print(A)
#>      [,1] [,2] [,3]
#> [1,]    1   -2    5
#> [2,]   -3    9    4
#> [3,]    5    0    6

Create the matrix B:

\[B = \begin{pmatrix} 2&-8& 14\\ 4&10&16\\ 6&12&18 \end{pmatrix}\]

B <- matrix(c(2, 4, 6, -8, 10, 12, 14, 16, 18), nrow = 3, ncol = 3, byrow = FALSE)

print(B)
#>      [,1] [,2] [,3]
#> [1,]    2   -8   14
#> [2,]    4   10   16
#> [3,]    6   12   18

2.6.2 Matrices slicing

Accessing elements in a matrix is done by using [row, column], between the square brackets, you indicate the position of the row and column in which the elements to access are. For example, to access the element in the first row and second column of matrix A, you type A[1, 2]. To access the element in the third row and second column of matrix A, you type A[3, 2].

A[1, 2] # Element in first row, second column
#> [1] -2
A[3, 2] # Element in third row, second column
#> [1] 0

2.6.3 Arithmetic Operation in Matrices

You can perform arithmetic operations on matrices. Consider the following matrices

\[A = \begin{pmatrix} 1&-2& 5\\ -3&9&4\\ 5&0&6 \end{pmatrix}\]

\[B = \begin{pmatrix} 2&-8& 14\\ 4&10&16\\ 6&12&18 \end{pmatrix}\]

A <- matrix(c(1, -3, 5, -2, 9, 0, 5, 4, 6), nrow = 3, ncol = 3, byrow = FALSE)
B <- matrix(c(2, 4, 6, 8, 10, 12, 14, 16, 18), nrow = 3, ncol = 3, byrow = FALSE)

Addition

A + B
#>      [,1] [,2] [,3]
#> [1,]    3    6   19
#> [2,]    1   19   20
#> [3,]   11   12   24

Multiplication

Matrix multiplication is done using %*% operator:

A %*% B
#>      [,1] [,2] [,3]
#> [1,]   24   48   72
#> [2,]   54  114  174
#> [3,]   46  112  178

2.6.4 Exercise 2.2.1: Matrix Transpose

Consider the following matrix \(A\):

\[A = \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{pmatrix}\]

Your Task:

Find the transpose of matrix \(A\), denoted as \(A^{T}\).

Tip

Define matrix \(A\), then use t(A) to find its transpose.

Here’s a starting point for your code:

# Define matrix A

A <- matrix(c(...), nrow = ..., ncol = ..., byrow = TRUE)

A_transpose <- ...(A)

Replace the ... with the correct values and complete the exercise!

See the Solution to Exercise 2.2.1

2.6.5 Exercise 2.2.2: Matrix Inverse Multiplication

Given the matrices \(A\) and \(B\) below:

\[A = \begin{pmatrix} 4 & 7 \\ 2 & 6 \end{pmatrix}\]

\[ B = \begin{pmatrix} 3 & 5 \\ 1 & 2 \end{pmatrix}\]

Your Task:

Calculate \(A^{-1} \times B\), where \(A^{-1}\) is the inverse of matrix \(A\).

Hint:

  • Use the solve() function in R to find the inverse of matrix \(A\).

  • Use the matrix multiplication operator %*% to multiply \(A^{-1}\) by \(B\).

Here’s a starting point for your code:

# Define matrices A and B
A <- matrix(c(...), nrow = ..., ncol = ..., byrow = TRUE)
B <- matrix(c(...), nrow = ..., ncol = ..., byrow = TRUE)

# Find the inverse of A
A_inverse <- solve(A)

# Multiply A_inverse by B
result <- A_inverse %*% B

Replace the ... with the correct values for your matrices and complete the exercise!

See the Solution to Exercise 2.2.2

2.6.6 Real-World Data Scenario: Sales Data Matrix

Suppose we have sales data for three products over four regions.

# Sales data (units sold)

sales_data <- c(500, 600, 550, 450, 620, 580, 610, 490, 530, 610, 570, 480)

# Create a matrix

sales_matrix <- matrix(sales_data, nrow = 4, ncol = 3, byrow = TRUE)

colnames(sales_matrix) <- c("Product_A", "Product_B", "Product_C")

rownames(sales_matrix) <- c("Region_1", "Region_2", "Region_3", "Region_4")

sales_matrix
#>          Product_A Product_B Product_C
#> Region_1       500       600       550
#> Region_2       450       620       580
#> Region_3       610       490       530
#> Region_4       610       570       480

Addition and Subtraction:

# Assume a competitor's sales matrix
competitor_sales <- matrix(
  c(
    480, 590, 540, 430, 610, 570,
    600, 480, 520, 600, 560, 470
  ),
  nrow = 4, ncol = 3, byrow = TRUE
)

competitor_sales
#>      [,1] [,2] [,3]
#> [1,]  480  590  540
#> [2,]  430  610  570
#> [3,]  600  480  520
#> [4,]  600  560  470
# Calculate the difference in sales

sales_difference <- sales_matrix - competitor_sales
sales_difference
#>          Product_A Product_B Product_C
#> Region_1        20        10        10
#> Region_2        20        10        10
#> Region_3        10        10        10
#> Region_4        10        10        10

Matrix Multiplication:

# Price per product
prices <- c(20, 15, 25)

# Calculate total revenue per region

revenue_per_region <- sales_matrix %*% prices
revenue_per_region
#>           [,1]
#> Region_1 32750
#> Region_2 32800
#> Region_3 32800
#> Region_4 32750

Accessing Elements:

# Sales of Product_B in Region_2
sales_matrix["Region_2", "Product_B"] # Returns 580
#> [1] 620
# All sales for Product_C
sales_matrix[, "Product_C"]
#> Region_1 Region_2 Region_3 Region_4 
#>      550      580      530      480
Common Pitfall
  • Dimension Mismatch:
    • Tip: Ensure that the number of columns in the first matrix matches the number of rows in the second for multiplication.

2.6.7 Reflection Question 2.2.1

  • In what scenarios would using a matrix be more advantageous than a data frame?

2.6.8 Practice Quiz 2.2

Question 1:

Which R function is used to find the transpose of a matrix?

  1. transpose()
  2. t()
  3. flip()
  4. reverse()

Question 2:

Given the matrix:

A <- matrix(1:6, nrow = 2, byrow = TRUE)

what is the value of A[2, 3]?

  1. 3
  2. 6
  3. 5
  4. 4

Question 3:

Matrix multiplication in R can be performed using the * operator.

  1. True

  2. False

Question 4:

What will be the result of adding two matrices of different dimensions in R?

  1. R will perform element-wise addition up to the length of the shorter matrix.
  2. An error will occur due to dimension mismatch.
  3. R will recycle elements of the smaller matrix.
  4. The matrices will be concatenated.

Question 5:

Which function can be used to calculate the sum of each column in a matrix M?

  1. rowSums(M)
  2. colSums(M)
  3. sum(M)
  4. apply(M, 2, sum)

Question 6:

Which function is used to create a matrix in R?

  1. matrix()
  2. data.frame()
  3. c()
  4. list()

See the Solution to Quiz 2.2

2.6.9 Exercise 2.2.3: Matrix Operations

Using the sales_matrix from the example in Section 2.6.6:

  1. Calculate the total units sold per product.
  2. Find the average units sold across all regions for Product_A.
  3. Identify the region with the highest sales for Product_C.

See the Solution to Exercise 2.2.3

2.7 Experiment 2.3: Data frame

A data frame is a two-dimensional data structure. It resembles a table, where variables are represented as columns, and observations are rows—much like a spreadsheet or a SQL table. Data frames allow you to store columns of different data types (e.g., numeric, character, logical), making them ideal for real-world datasets.

2.7.1 Creating a Data Frame

To create a data frame, use the data.frame() function.

Example 1: Sales Transactions Data Frame

# Sample sales transactions
transaction_id <- 1:5

product <- c("Product_A", "Product_B", "Product_C", "Product_A", "Product_B")

quantity <- c(2, 5, 1, 3, 4)

price <- c(19.99, 5.49, 12.89, 19.99, 5.49)

total_amount <- quantity * price

sales_transactions <- data.frame(
  transaction_id, product, quantity, price,
  total_amount
)

sales_transactions
#>   transaction_id   product quantity price total_amount
#> 1              1 Product_A        2 19.99        39.98
#> 2              2 Product_B        5  5.49        27.45
#> 3              3 Product_C        1 12.89        12.89
#> 4              4 Product_A        3 19.99        59.97
#> 5              5 Product_B        4  5.49        21.96

Notice the row numbers (1 2 3 4 5) displayed on the left of the console output—these are row labels. Each column in a data frame is internally represented as a vector.

Example 2: COVID 19 Data Frame

You can create a data frame for COVID-19 statistics with columns such as states, confirmed_cases, recovered_cases, and death_cases:

states <- c("Lagos", "FCT", "Plateau", "Kaduna", "Rivers", "Oyo")

confirmed_cases <- c(58033, 19753, 9030, 8998, 7018, 6838)

recovered_cases <- c(56990, 19084, 8967, 8905, 6875, 6506)

death_cases <- c(439, 165, 57, 65, 101, 123)

covid_19 <- data.frame(states, confirmed_cases, recovered_cases, death_cases)

covid_19
#>    states confirmed_cases recovered_cases death_cases
#> 1   Lagos           58033           56990         439
#> 2     FCT           19753           19084         165
#> 3 Plateau            9030            8967          57
#> 4  Kaduna            8998            8905          65
#> 5  Rivers            7018            6875         101
#> 6     Oyo            6838            6506         123

2.7.2 Exploring Data Frames

R provides several functions to quickly explore the structure and content of data frame (df):

  1. head(df): Displays the first few rows.

  2. tail(df): Displays the last few rows.

Both functions also include a “header”, showing the variable names in the data frame`.

  1. str(df): Shows the structure of the data frame, including:

    • Number of observations (rows) and variables (columns).

    • Variable names and data types.

    • A preview of the data in each column.

  2. names(df): Lists the names of the columns.

  3. nrow(df): Returns the number of rows.

  4. ncol(df): Returns the number of columns.

  5. dim(df): Returns the dimensions (rows and columns) as a vector.

  6. View(df): Opens a spreadsheet-style viewer in RStudio.

  7. summary(df): Provides summary statistics for all columns.

Example: Medical Data Frame

Consider the following vectors:

set.seed(2021) # Ensures reproducibility

gender <- sample(c("Male", "Female"), 120, replace = TRUE)

height <- floor(rnorm(n = 120, mean = 3, sd = 0.5))

weight <- ceiling(rnorm(n = 120, mean = 55, sd = 9))

bmi <- weight / height^2

medical_data <- data.frame(gender, height, weight, bmi)

Exploring the Medical Data Frame

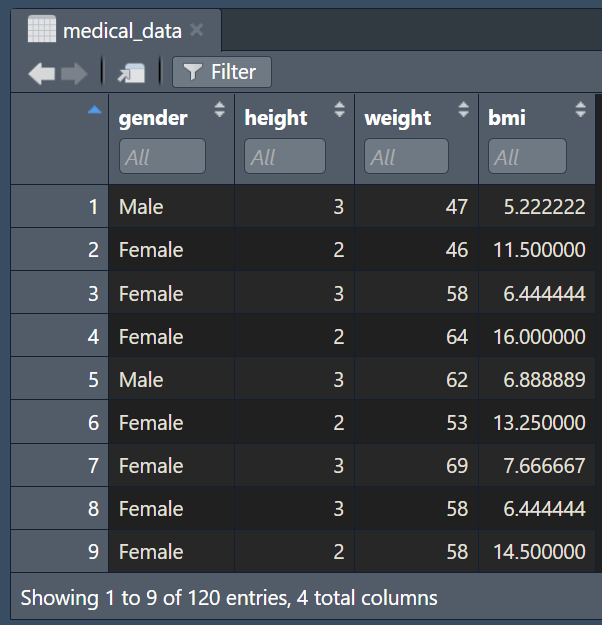
First six observations:

head(medical_data)
#>   gender height weight       bmi
#> 1   Male      3     47  5.222222
#> 2 Female      2     46 11.500000
#> 3 Female      3     58  6.444444
#> 4 Female      2     64 16.000000
#> 5   Male      3     62  6.888889
#> 6 Female      2     53 13.250000

Last six observations:

tail(medical_data) # To get the last 6 observation
#>     gender height weight       bmi
#> 115   Male      2     54 13.500000
#> 116   Male      3     66  7.333333
#> 117   Male      3     57  6.333333
#> 118   Male      3     49  5.444444
#> 119   Male      2     51 12.750000
#> 120 Female      3     51  5.666667

Column names:

names(medical_data)
#> [1] "gender" "height" "weight" "bmi"

You can also use:

colnames(medical_data)
#> [1] "gender" "height" "weight" "bmi"

View the data in RStudio (interactive):

View(medical_data)
A data frame preview in RStudio showing columns for gender, height, weight, and BMI (body mass index). The table includes both male and female entries, with height, weight, and calculated BMI values for each individual. The data illustrates how categorical and numerical values can be organized and analyzed in R.
Figure 2.4: Data Frame Preview in RStudio: Gender, Height, Weight, and BMI

Descriptive statistics:

summary(medical_data)
#>     gender              height          weight           bmi        
#>  Length:120         Min.   :1.000   Min.   :37.00   Min.   : 2.375  
#>  Class :character   1st Qu.:2.000   1st Qu.:50.00   1st Qu.: 6.333  
#>  Mode  :character   Median :2.000   Median :56.00   Median :11.000  
#>                     Mean   :2.433   Mean   :55.58   Mean   :12.384  
#>                     3rd Qu.:3.000   3rd Qu.:62.00   3rd Qu.:14.312  
#>                     Max.   :4.000   Max.   :78.00   Max.   :63.000

2.7.3 Built-in Datasets

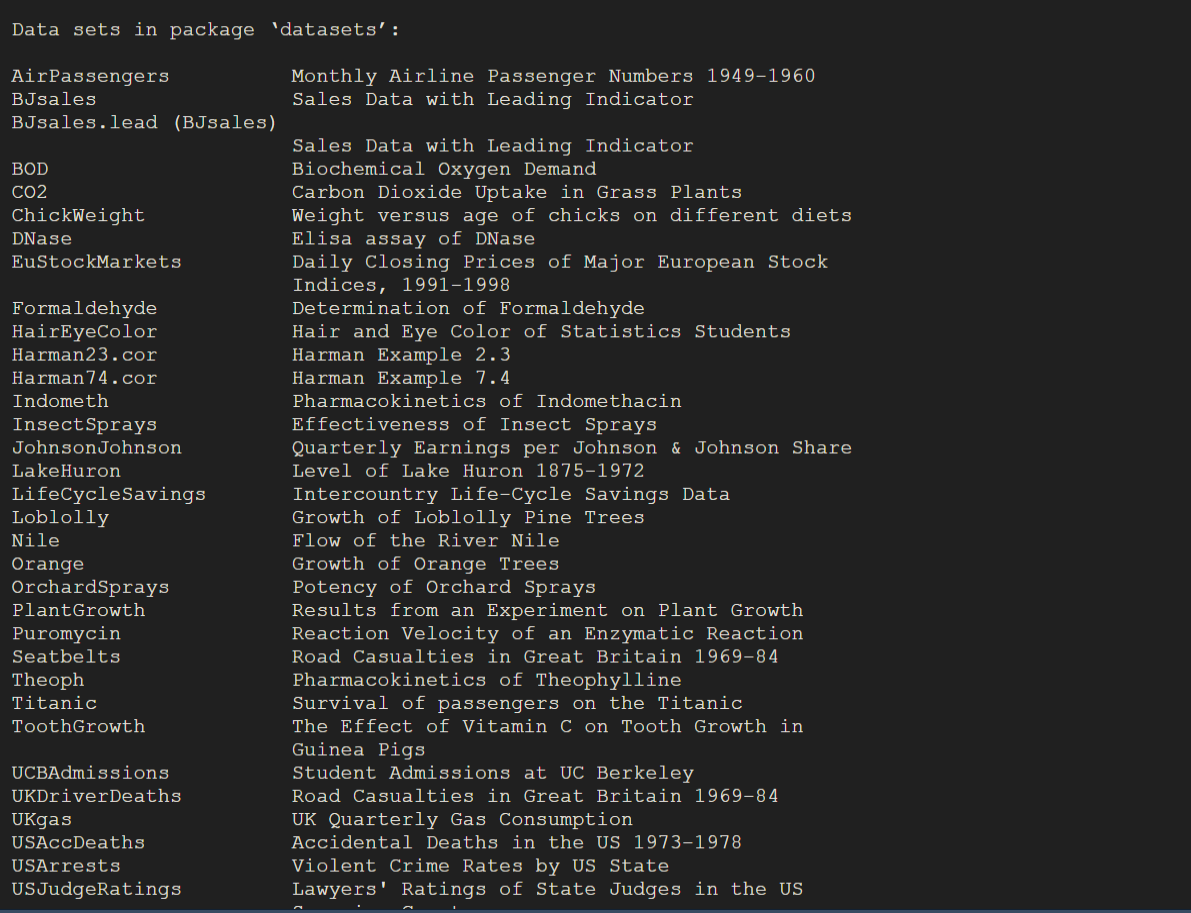
R comes with a variety of built-in datasets that you can use for learning, testing, or exploring data analysis techniques. To view the available datasets, use the following command:

This will open a list of all the datasets available in the datasets package. The datasets package provides a variety of datasets on different topics, such as biology, finance, and historical events. Figure 2.5 is an example output showing some of these datasets:

A terminal output listing various built-in datasets in the R 'datasets' package. Examples include 'AirPassengers' (monthly airline passenger numbers from 1949-1960), 'CO2' (carbon dioxide uptake in grass plants), 'Titanic' (survival of passengers on the Titanic), and many others covering topics such as biology, finance, and historical data. This list highlights the variety of real-world data readily available for analysis in R.
Figure 2.5: Sample Datasets Available in the R ‘datasets’ Package

2.7.3.1 Loading and Previewing Datasets

You can load and preview built-in datasets simply by calling their names. For example:

head(iris)
#>   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
#> 1          5.1         3.5          1.4         0.2  setosa
#> 2          4.9         3.0          1.4         0.2  setosa
#> 3          4.7         3.2          1.3         0.2  setosa
#> 4          4.6         3.1          1.5         0.2  setosa
#> 5          5.0         3.6          1.4         0.2  setosa
#> 6          5.4         3.9          1.7         0.4  setosa

This displays the first six rows of the iris dataset, which contains measurements of iris flowers.

head(airquality)
#>   Ozone Solar.R Wind Temp Month Day
#> 1    41     190  7.4   67     5   1
#> 2    36     118  8.0   72     5   2
#> 3    12     149 12.6   74     5   3
#> 4    18     313 11.5   62     5   4
#> 5    NA      NA 14.3   56     5   5
#> 6    28      NA 14.9   66     5   6

Here, the airquality dataset provides daily air quality measurements in New York from May to September 1973.

2.7.3.2 Getting Help on a Dataset

To learn more about a specific dataset, use the ? operator followed by the dataset name. For example:

?airquality

This will bring up the documentation for the airquality dataset as shown in Figure 2.6, which includes details about the variables, their format, and the source of the data.

A screenshot of the R documentation for the 'airquality' dataset, which provides daily air quality measurements in New York from May to September 1973. The dataset contains 153 observations on six variables: Ozone (ppb), Solar.R (Solar Radiation in Lang), Wind (mph), Temp (degrees Fahrenheit), Month (1-12), and Day (1-31). The documentation includes details about the data collection, usage, format, and sources of the dataset.
Figure 2.6: Airquality Dataset Documentation in R

2.7.4 Subsetting Data Frames

Every column in a data frame has a name. You can view the column names of a data frame, such as iris, by using the names() function:

names(iris)
#> [1] "Sepal.Length" "Sepal.Width"  "Petal.Length" "Petal.Width" 
#> [5] "Species"

2.7.4.1 Using the $ Operator

To access a specific column by name, use the $ operator in the format df$colname, where df is the name of the data frame and colname is the name of the column you want to retrieve. This operation returns the column as a vector. For example, to extract the Sepal.Length column from the iris data frame as a vector:

iris$Sepal.Length
#>  [1] 5.0 6.0 5.0 5.7 4.9 6.7 6.3 4.8 7.7 5.8 7.3 5.2 6.3 5.0 5.1 5.6 7.7 6.9
#> [19] 6.1 7.6

Similarly, to access the Species column:

iris$Species
#>  [1] setosa     versicolor virginica  setosa     virginica  setosa    
#>  [7] versicolor setosa     versicolor setosa     virginica  versicolor
#> [13] setosa     virginica  setosa     versicolor virginica  setosa    
#> [19] setosa     versicolor
#> Levels: setosa versicolor virginica
Note

For clarity and conciseness, we have shortened the output of both iris$Sepal.Length and iris$Species in the example outputs to save space. Both methods extract their respective columns as vectors.

Since the $ operator produces a vector, you can directly apply vector-based functions, such as mean(), sd(), or table(), to perform calculations on the column data.

For example:

  • To compute the mean of Sepal.Length:
mean(iris$Sepal.Length)
#> [1] 5.843333
  • To find the frequency of each Species:
table(iris$Species)
#> 
#>     setosa versicolor  virginica 
#>         50         50         50

2.7.4.2 Using [row, column] Notation

You can also subset data frames using [row, column], similar to matrices. In this syntax:

  • The row argument specifies which rows to extract.

  • The column argument specifies which columns to extract.

Here are some common examples and their interpretations, summarized in Table 2.1 below:

Table 2.1: Data Frame Slicing in R
Data Frame Slicing Interpretation
data[1, ] First row and all columns
data[, 2] All rows and second column
data[c(1, 3, 5), 2] Rows 1, 3, 5 and column 2 only
data[1:3, c(1, 3)] First three rows and columns 1 and 3 only
data or data[, ] All rows and all columns
Reflection Question 2.3.1

How does subsetting data frames help in data analysis?

Common Pitfalls
  • Undefined Columns Selected:
    • Tip: Use names(df) to verify column names before subsetting.
  • Incorrect Data Types:
    • Tip: Check data types with str(df) and convert if necessary.

2.7.5 Practice Quiz 2.3

Question 1:

Which function would you use to view the structure of a data frame, including its data types and a preview of its contents?

  1. head()
  2. str()
  3. summary()
  4. names()

Question 2:

How do you access the third row and second column of a data frame df?

  1. df[3, 2]
  2. df[[3, 2]]
  3. df$3$2
  4. df(3, 2)

Question 3:

In a data frame, all columns must contain the same type of data.

  1. True

  2. False

Question 4:

Which of the following commands would open a spreadsheet-style viewer of the data frame df in RStudio?

  1. View(df)
  2. view(df)
  3. inspect(df)
  4. display(df)

Question 5:

What does the summary() function provide when applied to a data frame?

  1. Only the first few rows of the data frame.
  2. Descriptive statistics for each column.
  3. The structure of the data frame including data types.
  4. A visual plot of the data.

Question 6:

In a data frame, all columns must be of the same data type.

  1. True

  2. False

See the Solution to Quiz 2.3

2.7.6 Exercise 2.3.1: Subsetting a Dataframe

Using the built-in airquality dataset, complete the following tasks:

  • Examine the airquality dataset.

  • Select the first three columns.

  • Select rows 1 through 3 and columns 1 and 3.

  • Select rows 1 through 5 and column 1.

  • Select the first row.

  • Select the first six rows.

See the Solution to Exercise 2.3.1

2.7.7 Exercise 2.3.2: Data Frame Manipulation

Using the sales_transactions data frame:

# Sample sales transactions
transaction_id <- 1:5

product <- c("Product_A", "Product_B", "Product_C", "Product_A", "Product_B")

quantity <- c(2, 5, 1, 3, 4)

price <- c(19.99, 5.49, 12.89, 19.99, 5.49)

total_amount <- quantity * price

sales_transactions <- data.frame(
  transaction_id, product, quantity,
  price, total_amount
)

sales_transactions
#>   transaction_id   product quantity price total_amount
#> 1              1 Product_A        2 19.99        39.98
#> 2              2 Product_B        5  5.49        27.45
#> 3              3 Product_C        1 12.89        12.89
#> 4              4 Product_A        3 19.99        59.97
#> 5              5 Product_B        4  5.49        21.96

  1. Add a new column discounted_price that applies a 10% discount to price.

  2. Filter transactions where the total_amount is greater than $50.

  3. Calculate the average total_amount for Product_B.

See the Solution to Exercise 2.3.2

2.8 Experiment 2.4: Lists

A list is an R object that can contain elements of different types—numbers, strings, vectors, and even other lists. It’s basically a container that can hold many different kinds of data structures.

You are already familiar with the notion of dimensions, such as the rows and columns in matrices and data frames. Unlike matrices or data frames, lists do not have the same concept of rows and columns. Instead, they are regarded as one-dimensional because they essentially consist of a sequence of items. You can think of it like a box full of different objects, all lined up one after the other.

2.8.1 Creating a List

To create a list, use the list() function:

# Customer Profile

customer_profile <- list(
  customer_id = 1001,
  name = "Johnny Drille",
  purchase_history = sales_transactions, # A data frame in Exercise 2.3.2
  loyalty_member = TRUE
)

customer_profile
#> $customer_id
#> [1] 1001
#> 
#> $name
#> [1] "Johnny Drille"
#> 
#> $purchase_history
#>   transaction_id   product quantity price total_amount
#> 1              1 Product_A        2 19.99        39.98
#> 2              2 Product_B        5  5.49        27.45
#> 3              3 Product_C        1 12.89        12.89
#> 4              4 Product_A        3 19.99        59.97
#> 5              5 Product_B        4  5.49        21.96
#> 
#> $loyalty_member
#> [1] TRUE

Here, customer_profile consists of four components:

  • customer_id: Numeric value.

  • name: Character string.

  • purchase_history: Data frame

  • loyalty_member: Logical value.

To check how many elements are in a list, you can use the length() function. For instance:

length(customer_profile)
#> [1] 4

2.8.2 Accessing List Elements

To show the contents of a list you can simply type its name as any other object in R:

customer_profile
#> $customer_id
#> [1] 1001
#> 
#> $name
#> [1] "Johnny Drille"
#> 
#> $purchase_history
#>   transaction_id   product quantity price total_amount
#> 1              1 Product_A        2 19.99        39.98
#> 2              2 Product_B        5  5.49        27.45
#> 3              3 Product_C        1 12.89        12.89
#> 4              4 Product_A        3 19.99        59.97
#> 5              5 Product_B        4  5.49        21.96
#> 
#> $loyalty_member
#> [1] TRUE

  • Using $ Operator:
    The $ operator is used to access elements of a list by their names. This method is straightforward and commonly used when you know the exact name of the element you want to access.

    customer_profile$name
    #> [1] "Johnny Drille"

  • Using Double Square Brackets [[ ]]:
    Double square brackets [[ ]] are used to extract elements from a list by their position (index) or name.

    customer_profile[[1]]
    #> [1] 1001
    customer_profile[["customer_id"]]
    #> [1] 1001

  • Using single square brackets []:
    Using single square brackets [ ] returns a list containing the element:

    customer_profile[1]
    #> $customer_id
#> [1] 1001
    customer_profile["customer_id"]
    #> $customer_id
#> [1] 1001

  • Accessing Data Frame within List:
    When a list contains a data frame (or another list), you can access elements within that data frame by chaining the $ operator or using a combination of [[ ]] and $.

    # Access the 'product' column in 'purchase_history'
customer_profile$purchase_history$product
    #> [1] "Product_A" "Product_B" "Product_C" "Product_A" "Product_B"
    # Access the amount of the second purchase
second_purchase_amount <- customer_profile$purchase_history$total_amount[2]

print(second_purchase_amount)
    #> [1] 27.45
Reflection Question 2.4.1
  • How can lists be used to organize complex data structures in R?
Common Pitfalls
  • Incorrect Indexing:
    • Tip: Remember that [ ] returns a sublist, while [[ ]] returns the element itself.

2.8.3 Practice Quiz 2.4

Question 1:

Which function is used to create a list in R?

  1. c()
  2. list()
  3. data.frame()
  4. matrix()

Question 2:

Given the list:

L <- list(a = 1, b = "text", c = TRUE)

how would you access the element "text"?

  1. L[2]
  2. L["b"]
  3. L$b
  4. Both b) and c)

Question 3:

Using single square brackets [] to access elements in a list returns the element itself, not a sublist.

  1. True

  2. False

Question 4:

How can you add a new element named d with value 3.14 to the list L?

  1. L$d <- 3.14
  2. L["d"] <- 3.14
  3. L <- c(L, d = 3.14)
  4. All of the above

Question 5:

What will be the result of length(L) if

L <- list(a = 1, b = "text", c = TRUE, d = 3.14)?

  1. 3
  2. 4
  3. 1
  4. 0

See the Solution to Quiz 2.4

2.8.4 Exercise 2.4.1: Working with Lists

Create a list named product_details that contains:

  • Product ID: 501
  • Name: “Wireless Mouse”
  • Specifications: A list containing color, battery_life, and connectivity
  • In Stock: TRUE

Access each element individually and the nested list.

See the Solution to Exercise 2.4.1

2.9 Experiment 2.5: Arrays

An array is a data structure used for storing data in more than two dimensions. It’s a bit like a matrix (which is two-dimensional), but arrays can extend to three dimensions or even more. In an array, all the elements must be of the same type (for example, all numeric or all character).

2.9.1 Creating Arrays

To create an array, use the array() function:

#|
array(data, dim = c(...), dimnames = NULL)

Where:

  • data: The elements to be arranged in the array (all of the same type).

  • dim: A vector specifying the dimensions of the array. For example, c(2, 3, 4) would create a three-dimensional array with dimensions 2 × 3 × 4.

  • dimnames: An optional argument where you can provide names for each dimension.

Example: Monthly Sales Data

Suppose we have sales data (in units sold) for two products across three regions over four months.

# Sales data for 2 products, across 3 regions, over 4 months

sales_vector <- c(
  50, 60, 55, 70, # Product A, Region 1, 4 months
  45, 52, 63, 65, # Product A, Region 2, 4 months
  80, 75, 70, 85, # Product A, Region 3, 4 months
  90, 95, 88, 92, # Product B, Region 1, 4 months
  55, 57, 59, 58, # Product B, Region 2, 4 months
  72, 78, 85, 80 # Product B, Region 3, 4 months
)
# Creating the 3D array (2 x 3 x 4)
sales_array <- array(
  data = sales_vector,
  dim = c(2, 3, 4),
  dimnames = list(
    Product = c("A", "B"),
    Region  = c("North", "East", "West"),
    Month   = c("Jan", "Feb", "Mar", "Apr")
  )
)

# Viewing the array
sales_array
#> , , Month = Jan
#> 
#>        Region
#> Product North East West
#>       A    50   55   45
#>       B    60   70   52
#> 
#> , , Month = Feb
#> 
#>        Region
#> Product North East West
#>       A    63   80   70
#>       B    65   75   85
#> 
#> , , Month = Mar
#> 
#>        Region
#> Product North East West
#>       A    90   88   55
#>       B    95   92   57
#> 
#> , , Month = Apr
#> 
#>        Region
#> Product North East West
#>       A    59   72   85
#>       B    58   78   80
Note

  1. Data
    The sales_vector contains all the numeric values we want to arrange in our array. Here, each element represents the number of units sold.

  2. Dimensions
    We pass dim = c(2, 3, 4) to specify that our array will have 2 rows (for the products), 3 columns (for the regions), and 4 “layers” (for the months).

  3. Dimension Names
    We optionally provide dimnames as a list of three vectors, each naming one dimension. This makes the final output more readable.

  4. Result
    The result is a 3D array in which you can access a single value or a “slice” of data by specifying the indices (for instance, sales_array["A", "East", "Feb"]).

Arrays are particularly useful when your data naturally extends beyond two dimensions—for instance, measuring different metrics across various categories and time periods. Just remember that all elements in an array must be of the same type (e.g., all numeric).

2.9.2 Reflection

Reflect on how arrays differ from other data structures in R. In what scenarios might you prefer using an array over a matrix, data frame, or list, and why?

Reflection Question 2.5.1

How does arrays differ from other data structures in R. In what scenarios might you prefer using an array over a matrix, data frame, or list, and why?

2.10 General Practice Quiz 2

Question 1

Which function is used to create a vector in R?

  1. vector()
  2. c()
  3. list()
  4. data.frame()

Question 2

Which function is used to create a matrix in R?

  1. array()
  2. list()
  3. matrix()
  4. data.frame()

Question 3

Which function is used to create an array in R?

  1. list()
  2. matrix()
  3. c()
  4. array()

Question 4

Which function is used to create a list in R?

  1. list()
  2. c()
  3. matrix()
  4. data.frame()

Question 5

A matrix in R must contain elements of:

  1. Multiple data types (e.g., numeric and character mixed)
  2. Only character type
  3. Only logical type
  4. The same type (all numeric, all logical, etc.)

Question 6

An array in R can be:

  1. Only two-dimensional
  2. Only one-dimensional
  3. Two-dimensional or higher
  4. Unlimited in one dimension only

Question 7

A list in R is considered:

  1. Two-dimensional
  2. One-dimensional
  3. Multi-dimensional
  4. A type of matrix

Question 8

Which of the following is TRUE about a list?

  1. It can only contain numeric data
  2. It stores data with rows and columns by default
  3. It can store multiple data types in different elements
  4. It must be strictly two-dimensional

Question 9

What is the most suitable structure for storing heterogeneous data (e.g., numbers, characters, and even another data frame) in a single R object?

  1. Vector
  2. Matrix
  3. Array
  4. List

Question 10

How do we typically check the “size” of a list in R?

  1. nrow()
  2. length()
  3. dim()
  4. ncol()

Question 11

Which function is used to create a data frame in R?

  1. data.frame()
  2. array()
  3. c()
  4. list()

Question 12

A data frame in R:

  1. Must be strictly numeric
  2. Can store different data types in each column
  3. Is always one-dimensional
  4. Is identical to a matrix

Question 13

If you want to assign dimension names to an array, you should use:

  1. rownames() only
  2. colnames() only
  3. dimnames()
  4. names()

Question 14

When creating a matrix using:

matrix(1:6, nrow = 2, ncol = 3, byrow = TRUE)

How are the elements placed?

  1. Filled by columns first
  2. Filled by rows first
  3. Randomly placed
  4. Not possible to tell

Question 15

In an array with dimensions c(2, 3, 4), how many elements are there in total?

  1. 12
  2. 18
  3. 24
  4. 36

See the Solution to General Quiz 2

2.11 Reflective Summary

Congratulations on completing Lab 2! You’ve expanded your R programming skills by mastering essential data structures:

  • Vectors: The building blocks of data manipulation.

  • Matrices: Fundamental for mathematical and statistical computations.

  • Data Frames: Crucial for handling and analyzing real-world datasets.

  • Lists: Versatile structures for complex data storage.

Key Takeaways:

  • Understanding the appropriate data structure to use based on the data and task at hand is crucial.

  • Effective data manipulation relies on mastering indexing and subsetting techniques.

  • Combining different data structures allows for more complex data analyses.

What’s Next?

In the next lab, you’ll explore how to write your own functions in R. Functions are powerful tools that will help you streamline your code, automate tasks, and make your programs more efficient.

  1. The c() function is used to combine or concatenate values into a vector. It serves as a fundamental tool for creating vectors of various data types, such as numeric, character, or logical values.↩︎